一、矩形
1、定义：我们把有一个角是直角的平行四边形叫做矩形。
例如：长方形、正方形。
2、性质定理：（具有与普通平行四边形相同的性质+本身的特性）
①矩形的对边相等。（平行四边形的定义、三角形全等）
②矩形的对角相等且每个角为90°。（矩形的定义、三角形全等）
③夹在两条平行线间的平行线段相等。（平行四边形的定义）
④夹在两条平行线间的垂线段相等。（平行线之间的距离、平行四边形的定义）
⑤矩形的对角线互相平分且相等。（平行四边形的定义、三角形全等）
3、判定定理：
①有一个角是直角是平行四边形是矩形。（矩形的定义）
②有三个角是直角的四边形是矩形。（平行线的判定、三角形全等）
证明如下：（利用平行线的判定来解决）
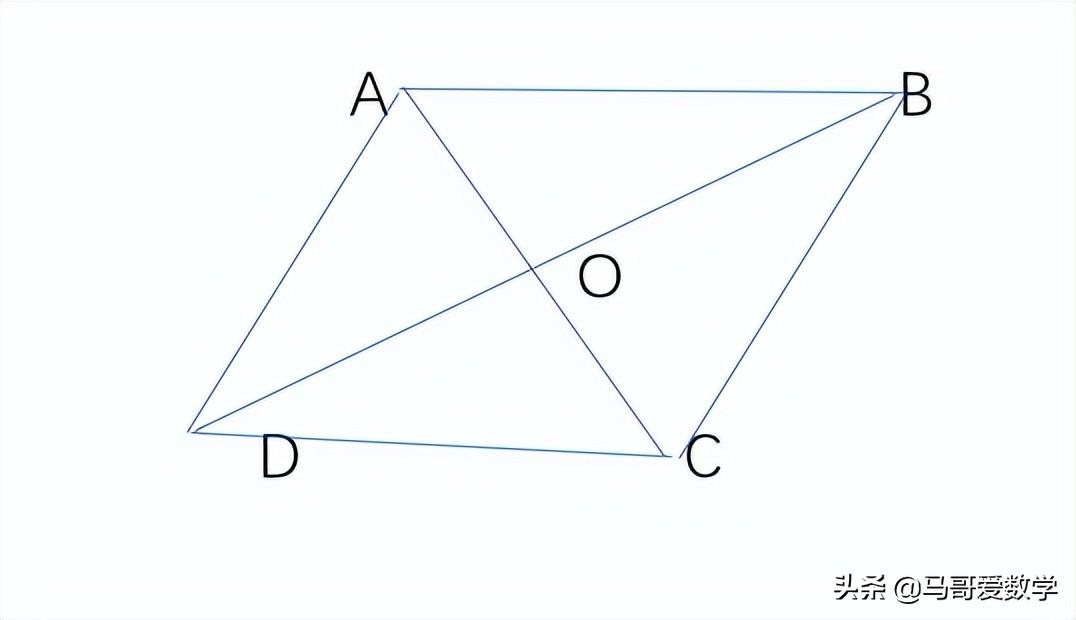
因为∠A=∠B=∠C=∠D=90°，所以AD∥BC,AB∥CD，四边形ABCD为平行四边形。
再次根据已知条件，平行四边形ABCD为矩形。
③对角线相等的平行四边形是矩形。（平行线的性质、三角形全等）
证明如下：（三角形全等）
上图中，平行四边形ABCD的对角线AC=BD，
因为AD∥BC，AD=BC，所以∠C+∠D=180°,
又因为，△ADC≌△BCD（证明略），所以∠C=∠D=90°，平行四边形ABCD为矩形。
二、菱形
1、定义：我们把一组邻边相等的平行四边形叫做菱形，它也是轴对称图形，对称轴为它的两条对角线。
例如：正方形（特殊的菱形）。
2、性质定理：（具有与普通平行四边形相同的性质+本身的特性）
①菱形的对边相等且四条边都相等。（平行四边形的性质定理、菱形的定义、三角形全等）
②菱形的对角相等。（平行四边形的性质定理、三角形全等）
③夹在两条平行线间的平行线段相等。（平行四边形的定义）
④夹在两条平行线间的垂线段相等。（平行线之间的距离、平行四边形的定义）
⑤菱形的对角线互相垂直且平分，每条对角线平分一组对角。（平行四边形的性质定理、三角形全等）
3、判定定理：
①四条边相等的四边形是菱形。（三角形全等）
证明：只要证明由公共边是一条对角线的两个三角形全等，即可推出四边形是平行四边形，所以，四条边相等的四边形是菱形。
②对角线互相垂直的平行四边形是菱形。（三角形全等）
证明：只要证明有对顶角的两个三角形全等，即可推出对角线互相平分，所以，两个有公共对角线的直角三角形的斜边相等（#勾股定理#），即可证明，对角线互相垂直的平行四边形是菱形。
三、正方形
1、定义：我们把有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形，它既是特殊的矩形，也是特殊的菱形。
2、性质定理：（具有平行四边形、矩形、菱形的公共性质和单独的特性）
正方形的特性：①正方形的四个角都是直角，四条边相等。（菱形的性质定理、正方形的特性）
②正方形的对角线相等且互相垂直平分，每条对角线平分一组对角。（菱形的性质定理、三角形全等、菱形的特性）
3、判定定理：
①有一组邻边相等的矩形是正方形。（正方形的定义）
②有一个角是直角的菱形是正方形。（正方形的定义）
③对角线互相垂直的矩形是正方形。（正方形的定义的推广）
④对角线相等的菱形是正方形。（正方形的定义的推广）
数与形总是分不开的
相关文章：
威廉斯壁挂炉用户售后客服中心实时反馈全+境+到+达04-26
昌宇燃气灶售后服务中心号码售后服务网点实时反馈-今-日-汇-总04-26
一洲壁挂炉全国各市24小时售后服务点热线号码实时反馈-今-日-汇-总04-26
乐时芬德壁挂炉售后维修号码-人工售后号码实时反馈-今-日-汇-总04-26
纽恩泰空气能24小时售后服务热线实时反馈-今-日-更-新04-26
盼盼乐热水器售后故障维修客服服务热线是多少实时反馈-今-日-汇-总04-26